ISLLg - 4TTA - E02
Les résistances

La résistance des conducteurs

Nous avons vu que le courant électrique résultait d'un mouvement ordonné de charges électriques. Dans les métaux, ce sont les électrons qui se déplacent, mais ils sont freinés dans leur déplacement (par exemple lors de collisions lors du passage d'un grain métallique à son voisin). La conséquence de ce phénomène est que si l'on applique une différence de potentiel aux bornes d'un conducteur, le courant qui y circule n'est pas infini. Plus précisément, il augmentera si la différence de potentiel augmente.

Définition de la résistance électrique

On appelle résistante électrique, un récepteur tel que le courant qui le traverse est proportionnel à la ddp appliquée à ses bornes.

Représentation

Il existe 2 sortes de résistances électriques
Valeurs fixes.


Valeurs variables, appelées aussi «rhéostats » ou «potentiomètres ».


Unité et mesure

Symbole : R.
Unité : Ω (Ohm).        Multiple : kΩ  et MΩ.    Sous-multiple : mΩ.

Mesure de la résistance électrique.
Appareil utilisé : l’ohmmètre.       
Raccordement : en parallèle sur l’élément à mesurer.


La loi d’Ohm

À résistance constante (R), si le courant (I) augmente, la tension (U) augmente aussi.  On dit que la tension et le courant sont proportionnels.
Si la tension est constante, la résistance détermine la valeur du courant, on peut dire que si la résistance augmente, l’intensité diminue et inversement.

U = R * I

U = valeur de la tension mesurée en V
R = valeur de la résistance en Ω
I = valeur de l’intensité du courant électrique en A

Attention : seules les résistances répondent à la loi d'Ohm, il existe d'autres composants électriques et électroniques qui ne suivent pas cette loi : diodes, moteurs, batteries, condensateurs...


Fabrication et calcul de résistances

Les résistances sont généralement fabriquées avec un fin fil métallique résistif (ou anciennement du carbone) qui est bobiné sur un noyau isolant pour réduire son encombrement. Il est possible de calculer la valeur de la résistance à partir des dimensions du fil et de la propriété électrique du conducteur qui le constitue.

La résistivité électrique

La résistivité d’un matériau est un coefficient qui le caractérise au point de vue de sa résistance électrique.

Caractéristique de la résistivité électrique.
Symbole : ρ.        Unité : Ωmm²/m  ou  Ωm²/m  donc  Ωm

Valeurs de résistivités électriques.
Ag : ρ = 0,016 Ωmm²/m  =  16 x 10–9 Ωm
Cu : ρ = 0,017 Ωmm²/m  =  17 x 10–9 Ωm    (à connaître de mémoire)
Alu : ρ = 0,028 Ωmm²/m  =  28 x 10–9 Ωm
Ni : ρ = 0,070 Ωmm²/m  =  70 x 10–9 Ωm
Fe : ρ = 0,104 Ωmm²/m  =  104 x 10–9 Ωm
Pb : ρ = 0,207 Ωmm²/m  =  207 x 10–9 Ωm
Carbone : ρ = 35,0 Ωmm²/m  =  35 x 10–6 Ωm

La loi de Pouillet

La valeur de la résistance électrique est :

R = ρ * L / S
ou
R * S = ρ * L

R = résistance en Ω                           
ρ = résistivité du fil (nature du fil) en Ωmm²/m ou en Ωm
L = longueur du fil résistant en m                  
S = section du fil résistant en mm² ou en m²

Attention :
Si vous utiliser S en mm² vous devez utiliser ρ en Ωmm²/m
Si vous utiliser S en m² vous devez utiliser ρ en Ωm

Rappel :
Les conducteurs ont généralement une forme cylindrique, leur section est alors un disque.  Pour calculer la section d’un fil, il faut connaître, soit son rayon, soit son diamètre. La formule permettant de calculer la section d’un fil sera donc :

S = π * r²    ou    S = π * d² / 4

NB : il existe des jauges de contraintes, qui permettent ce convertir des variations de L en variation de R

Echauffement des résistances

La température

La température, c'est la mesure de l'agitation thermique des particules d'un corps. Au 0 absolu (0°K = -275.15°C), les particules sont immobiles. Plus la température du corps augmente, plus ses particules sont en vibration. Si la température augmente jusqu'à un certain seuil, l'agitation est telle que le corps devient liquide (fusion). Si la température augmente encore, l'agitation est telle que le corps devient gazeux (évaporation).

Plus d'infos sur : http://fr.wikipedia.org/wiki/Température

La résistivité d'un matériau résulte des collisions des électrons dans ce conducteur. Ces collisions augmentent l'énergie vibratoire des particules du conducteur. La température du conducteur augmente. Il y a donc conversion d'énergie électrique en énergie calorifique.

L'effet Joule

Toute résistance traversée par un courant électrique s'échauffe. Dans une résistance, toute l'énergie électrique perdue au travers de la résistance est transformée en énergie calorifique (rendement de 100%).

On appelle effet Joule la transformation, par une résistance, de l’énergie électrique en énergie calorifique.

Les expériences de Monsieur Joule (chauffage d'eau avec une résistance) lui ont permis de dire que la puissance dissipée dans une résistance est donnée par les formules suivantes (transformation via la loi d'Ohm U = R * I) :

P = R * I²
P = U² / R
P = U * I

Où
P = puissance en W  (Watt)
R = résistance en Ω
I = courant en A
U = tension en V

Nous verrons que cette dernière formule P= U * I est la formule générale de la puissance en électricité.

Attention, chaque resistance a une puissance maximale (donnée par le fabriquant). Cette puissance dépend des capacités de refroidissement de la résistance. Ce refroidissement peut se faire par une circulation d'air (ex : sèche cheveux), d'eau (ex : chauffe-eau), par rayonnement (lampe à incandescence)... Si cette puissance est dépassée, la résistance brûle ou fond (principe des anciens fusibles en fil de plomb).

Environnement et économie : Si le rendement des résistances est de 100%, le rendement des centrales électriques est généralement inférieur à 40%. Il faut au final produire 3 quantités de chaleur dans la centrale pour en obtenir 1 dans la résistance. Le chauffage électrique est de ce fait coûteux et polluant. Il doit donc être réservée à des applications spécifiques (régulation précise, très haute température, utilisation occasionnelle...).

Loi de Matthiessen

Lorsque la température d'un conducteur augmente, l'augmentation de l'agitation thermique de ses particules augmente les probabilités de collisions des électrons avec la matière : la résistivité augmente avec la température. Il existe d'ailleurs des supraconducteurs qui ont une résistivité nulle vers -270°C. Dans les métaux cette variation suit une formule parabolique en fonction de la température, mais il existe une approximation linéaire pour les faibles écarts de température : la loi de Matthiessen.

ρT = ρ0 (1 + α(T - T0))
RT = R0 (1 + α(T - T0))
T = T0 + ((RT/R0) - 1)/α

ρT = résistivité en  Ωm à la température finale T en °C
ρ0 = résistivité en  Ωm à la température de départ T0 en °C.
RT = résistance en  Ω à la température finale T en °C
R0 = résistance en  Ω à la température de départ T0 en °C.
α = coefficient de température, dépend du matériau, en °C–1.

Quelques coefficients de température
Argent : α = 0,0038 °C–1
Cuivre : α = 0,0043 °C–1
Aluminium : α = 0,0043 °C–1
Fer : α = 0,0025 °C–1
Constantan : α = 0,00001 °C–1
Tungstène : α = 0,0065 °C–1
Carbone : α = -0,0004 °C–1

NB : il existe des semi-conducteurs à coefficient de température négatif, très sensible sur une plage de température (α important), utilisé notamment pour la mesure précise de température.


Groupements de résistances

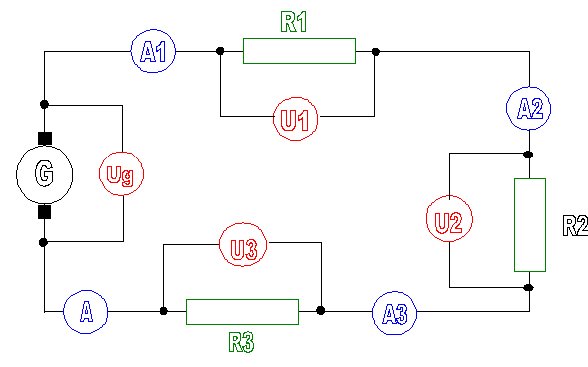
Montage série

Un montage série veut dire placer les récepteurs les uns après les autres ou encore relier la sortie d’un récepteur avec l’entrée de l’autre.

C'est le même courant qui traverse chaque résistance, d'où (via la loi d'Ohm) :

Req = R1 + R2 + R3

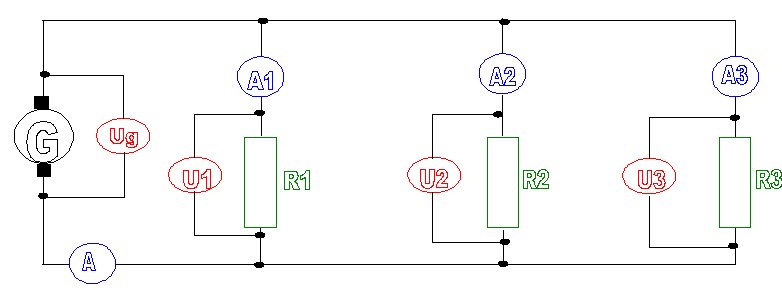
Montage parallèle

Un montage parallèle veut dire placer les récepteurs les uns à côté des autres pour que les entrées soient reliées ensemble ainsi que les sorties.

C'est la même tension qui est appliquée à chaque résistance, d'où (via la loi d'Ohm) :

1/Req = 1/R1 + 1/R2 + 1/R3

Diviseur potentiométrique

Le glissement du curseur d'un potentiomètre peut être modélisé par un circuit série à 2 résistances :

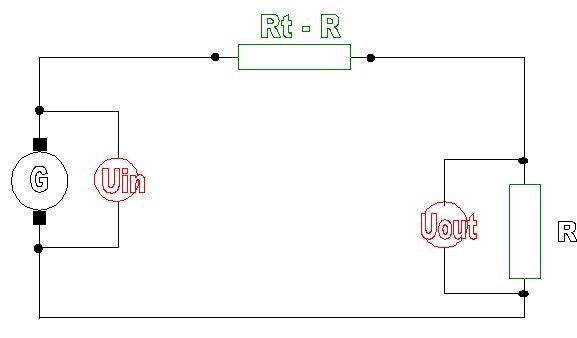Uout = Uin * R/Rt


Uin = tension appliquée aux extrémités du potentiomètre
Rt = résistance totale aux extrémités du potentiomètre 
R = résistance au niveau du curseur  (R < Rt)
Uout = tension lue au niveau du curseur du potentiomètre

Potentiomètre au minimum :     R = 0        =>  Uout = 0V
Potentiomètre à mi-course :      R = Rt/2    =>  Uout = Uin/2
Potentiomètre à fond :               R = Rt       =>  Uout = Uin

Application : réglage d'une tension de référence, réglage du volume d'une chaîne Hi-Fi...
Auteur : Marc PHILIPPOT - Version du 15/09/2011