ISLLg - 4TTA - E06
Groupements
de générateurs. Puissance et rendement.
Comme les résistances,
les générateurs peuvent être groupés en série, en parallèle ou
en montage mixte. Dans ce chapitre, nous allons voir les effets de ces
groupements sur la tension de sortie, la résistance interne et le
courant de court-circuit. Nous verrons également comment calculer la
puissance maximale et le rendement d'un générateur.
Les groupements
Le montage série
Dans le montage série, les pôles de noms contraires sont reliés entre
eux.

Via la loi des tensions du montage en série : la f.é.m. du
montage série est égale à la somme des f.é.m. partielles :
Eeq
= E1 + E2 + E3
Via la loi des résistances en série : la
résistance interne du montage série est égale à la somme des
résistances partielles :
Rgeq = Rg1 + Rg2 + Rg3
Concernant la quantité d'électricité, c'est un peu plus complexe, elle
va être limitée par celle du générateur le plus faible :
Qeq = minimum(Q1, Q2, Q3)
C'est pour cette raison que l'on met généralement des
générateurs
identiques en série.
Groupement de "s" générateurs identiques en série :
Eeq
= s * E
Rgeq = s * Rg
Icceq = Icc
Qeq = Q
Le montage série permet d'augmenter la tension de sortie ; mais ni le
courant max, ni la quantité d'électricité.
Le montage parallèle
Dans le montage parallèle, les pôles de mêmes noms sont reliés entre
eux.
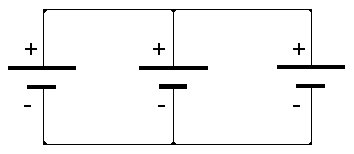
Pour ne pas créer de court-circuits entre les générateurs, il est
impératif qu'ils aient tous la même f.é.m.
C'est pour cette raison que l'on met généralement des générateurs
identiques en parallèle.
Via la loi des tensions du montage en parallèle :
la f.é.m. du montage parallèle est égale aux f.é.m. partielles :
Eeq
= E1 = E2 = E3
Via la loi des résistances en parallèle : la
conductance (1/R) interne du montage parallèle est égale à la
somme des conductances partielles :
1/Rgeq = 1/Rg1 + 1/Rg2 +
1/Rg3
Quant à la quantité d'électricité du montage, elle
est égale à la somme des quantités d'électricité
patielles :
Qeq = Q1 + Q2
+ Q3
Groupement de "p" générateurs identiques en parallèle :
Eeq
= E
Rgeq = Rg/p
Icceq = p * Icc
Qeq = p * Q
Le montage parallèle permet d'augmenter le courant
max et la quantité d'électricité ; mais pas la tension de
sortie.
Le montage mixte
Il
est utilisé lorsque l'on veut à la fois augmenter la tension de sortie,
ainsi que le courant et la quantité d'électricité.
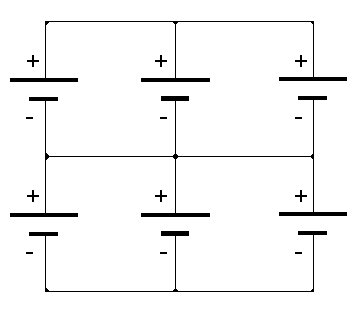
Groupement de "p" branches en parallèle de "s" générateurs
identiques en série :
Eeq
= s * E
Rgeq = Rg * s/p
Icceq = p * Icc
Qeq = p * Q
Puissance d'un générateur
On
appelle puissance utile (Pug), ou puissance aux bornes d’un générateur,
la puissance qu’il fournit à son circuit de charge. Certains récepteurs
ont des propriétés différentes de celles des résistances, mais quelle
que soit le nature du circuit de charge, la puissance utile (Pug) d’un
générateur fournissant le courant I sous la tension U se calcule par la
formule générale P = U * I.
A partir des valeurs de tension et de courant mesurés pour le tracé de
la caractéristique tension-courant on calcul la puissance utile du
générateur et on représente graphiquement cette puissance en fonction
du courant.
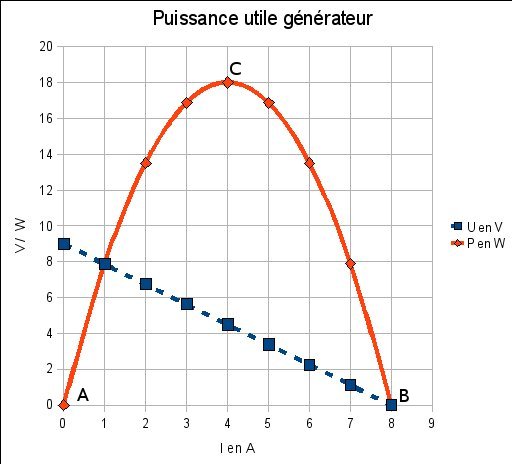
Constatation
La forme de la caractéristique de la puissance est une parabole.
La valeur de la puissance démarre d’un minimum, passe par un maximum et
revient vers un minimum.
La valeur du courant pour la puissance maximum vaut la moitié de Icc.
La valeur de la tension correspondant à ce Icc/2, vaut E/2.
Explication
U = E - Rg * I => P = E * I - Rg * I²
Point A:
I = 0A ; U = E ; car le générateur est à vide.
Calcul de la puissance : Pug = 0W car I = 0 A.
Point B :
I = Icc ; U = 0V.
Calcul de la puissance : Pug = 0 W car U =
0 V.
Point C :
I = Icc/2 ; U = E/2.
Calcul de la puissance : Pug = E * ICC / 4
= E² / 4Rg.
Que vaut la valeur de la résistance de charge R au point C ?
R = U / I = (E/2) / (Icc/2) = (E/2) /
(E/2Rg) = Rg .
Donc on peut dire que la puissance du générateur sera maximum lorsque R
= Rg .
Ce phénomène s’appelle : adaptation de la résistance de charge
R au générateur.
Formule
Pmax
= E² / (4 * Rg)
lorsque R = Rg ; I = Icc/2 ; U = E/2.
Les panneaux photovoltaïques
Ce
fonctionnement à Pmax ne peut généralement être maintenu qu'un court
instant (quelques secondes) avec les générateurs électro-chimiques ou
électro-mécaniques ; en effet, le maintien de ce courant élevé (Icc/2)
conduirait à des échauffements internes excessifs et la destruction du
générateur.
Par contre, pour les cellules photovoltaïques, on
recherche à amortir leurs coûts de fabrication et d'installation en un
minimum de temps : il faut donc en tirer la puissance maximale. Vu la
grande surface de ces panneaux exposés à l'air libre, il n'y a pas de
problème d'échauffement si on les fait fonctionner en continu à Pmax.
Technologies actuelles
(par rendement et prix décroissants) : silicium monocristallin, silicium
polycristallin, silicium amorphe... mais il y a de nombreuses recherches
en cours.
Coût : de 5€ (grands panneaux) à 10€ (petits panneaux) par Watt.
Comparaison du prix du kWh :
Réseau électrique :
0.20€/kWh
Photovoltaïque : 0.40 à 0.60€/kWh (mais certificats verts à
déduire)
Piles chimiques : 20.00 à 1500.00€/kWh
Les
équipements à piles ont donc tout intérêt à être remplacé par du photovoltaïque (plus léger, moins coûteux et polluants)
dès qu'ils sont utilisés plus de
2 à 5 minutes chaque jour.
Caractéristiques d'un panneau
Un
panneau photovoltaïque est caractérisé par deux grandeurs : sa tension
à vide "E" en plein soleil et son courant maximum "Icc" en plein soleil.
Sa
puissance maximale en plein soleil serait alors : Pmax = E * Icc / 4
(en réalité, voir remarque 4 : Pmax =
0.56 * E *
Icc)
Vu qu'une cellule photovoltaïque a une tension de sortie de 0.6V, la
tension à vide peut aussi se calculer par :
E = s * 0.6V
où s est le nombre de cellules mises en série.
E varie peu à lumière ambiante.
Par
contre Icc est directement proportionnel à la surface des cellules et
la puissance lumineuse reçue (plein soleil, soleil voilé, nuageux...).
Choix du bon panneau
Pour recharger une batterie à une tension U avec un courant I, il faut
choisir un panneau tel que :
E = 2 * U (en réalité, voir remarque 4
: E = 1.60 * U)
Icc = 2 * I (en réalité, voir remarque
4 : Icc = 1.15 * I)
Exemple : batterie 12V à recharger à 2A, il faut un panneau de 25W /
24V - 4A (soit 40 cellules 0.6V-4A en série).
Remarques
1)
Le panneau ne doit pas être partiellement à l'ombre, c'est la cellule
la moins bien éclairée qui va déterminer le Icc vu qu'elles sont toutes
en série.
2) Le panneau doit être perpendiculaire aux rayons du soleil.
3)
Il faut un petit accumulateur (avec protection contre les surcharges)
ou un régulateur électronique de tension pour ne pas que la tension de
sortie double lorsque la consommation de courant diminue.
4) La relation U/I n'est pas une droite pour les cellules
photovoltaïques, le courant réel de travail sera supérieur à Icc/2.
Les fabricants donnent généralement le point optimal de fonctionnement
à Pmax : Uopt = 0.64 * E / Iopt = 0.88 * Icc
Rendement électrique d'un générateur
Nous avons vu que la puissance utile du générateur est égale à : Pug = U * I.
La puissance électrique consommée dans le générateur est égale à : Pa = E * I.
La différence est dissipée en chaleur dans le générateur (effet Joule dans Rg).
Le rendement est donné par :
η = Pug / Pa soit
η = U/E
Lorsque
le générateur est chargé par une résistance, on sait que la tension aux
bornes de la résistance vaut U = R x I et que la f.é.m. vaut E = (R +
rg) x I. Le rendement électrique devient :
η = (R x I) / ((R + rg) x I) soit
η = R / (R + rg)
Dans le cas d’un générateur adapté, on sait que rg = R. Dés
lors, η = R / 2R = 50%.
Hormis
pour les panneaux photovoltaïques, on essaye toujours d'avoir un bon
rendement (supérieur à 90%). Pour cela il faut que U reste proche de E
(max 10% de chute), c-à-d que Rg doit être petite par rapport à R (au
moins 9 fois plus petite). Il faut donc un générateur avec un Rg
suffisament faible ou alors mettre des générateurs en parallèle pour
diminuer Rg.
Pour les piles et accumulateurs, il n'y
a généralement pas de problème de rendement tant que l'on garantit
un minimum de 2H d'autonomie (Q et Rg sont en effet étroitement liés).
NB : Pour avoir le rendement global du générateur, il faut multiplier ce rendement électrique par
- le rendement de charge dans le cas d'un accumulateur,
- le rendement mécanique dans le cas d'une dynamo ou d'un alternateur.
Le rendement global sera donc toujours inférieur au rendement électrique calculé ci-dessus.
Auteur :
Marc PHILIPPOT - Version du 05/03/2012



