ISSLg
- Cours d'électronique
Les règles de
l'algèbre de Boole
Navigation> electronique/automatisme/portes/algebre
Pour plus de détails,
voir Floyd - Systèmes numériques - 9ème édition :
p182 : Chap 4 : Algèbre
booléenne et simplification logique
Principales règles en logique
Nous avons déjà vu l'associativité, la commutativité et la
distributivité.
Idempotence
A + A = A
A . A = A
Éléments neutres
A + 0 = A
A . 1 = A
Absorption
A + 1 = 1
A . 0 = 0
Complémentarité
//A = A
A . /A = 0
A + /A = 1
Simplification
A + /A . B = A + B
A . (/A + B) = A . B
Première loi de De Morgan (NOR)
/(A + B) = /A . /B
Deuxième loi de De Morgan (NAND)
/(A . B) = /A + /B
Le passage d'une table de vérité à
une équation
A chaque ligne d'une table de vérité correspond une équation :
| C |
B |
A |
équation de la ligne
|
| 0 |
0 |
0 |
/A . /B . /C |
| 0 |
0 |
1 |
A . /B . /C |
| 0 |
1 |
0 |
/A . B . /C |
| 0 |
1 |
1 |
A . B . /C |
| 1 |
0 |
0 |
/A . /B . C |
| 1 |
0 |
1 |
A . /B . C |
| 1 |
1 |
0 |
/A . B . C |
| 1 |
1 |
1 |
A . B . C |
Il suffit en suite de faire des OR des équations des lignes pour lesquelles la sortie Q est à 1 :
Exemple :
| C |
B |
A |
| Q | équation de la ligne
|
| 0 |
0 |
0 |
| 0 | /A . /B . /C |
| 0 |
0 |
1 |
| 0 | A . /B . /C |
| 0 |
1 |
0 |
| 1 | /A . B . /C |
| 0 |
1 |
1 |
| 0 | A . B . /C |
| 1 |
0 |
0 |
| 0 | /A . /B . C |
| 1 |
0 |
1 |
| 1 | A . /B . C |
| 1 |
1 |
0 |
| 0 | /A . B . C |
| 1 |
1 |
1 |
| 1 | A . B . C |
Q = /A . B . /C + A . /B . C + A . B . C
Ensuite, on simplifie si possible cette équation :
Q
= /A . B . /C + A . /B . C + A . B . C = /A
. B . /C + A . C (/B + B) = /A . B . /C + A
. C
Que l'on peut finalement convertir en combinaison de portes :
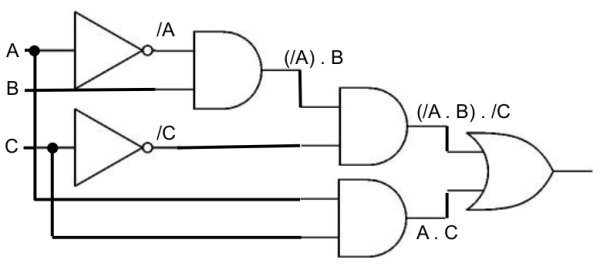
NB
: si la table de vérité comporte une sortie avec moins de ligne à 0 que
à 1, il est plus simple de travailler comme ci-dessus avec les lignes à
0 et de faire la négation (NOT) de la solution.
