ISSLg - Cours d'électronique
La combinaison de signaux logiques
Navigation> electronique/automatisme/logique/combinatoire
La combinatoire avec des contacts
Le OUI (ou buffer)
En schématique :
Avec une table de vérité : | SW1 | | L1 |
| relaché | 0 | | éteinte | 0 |
| poussé | 1 | | allumée | 1 |
En Français :La lampe L1 est allumée si le bouton SW1 est poussé.
(En binaire : La sortie est identique à l'entrée)
En algèbre de Boole :L1 = SW1En langage de programmation Pascal :l1 := sw1;En portes américaines :entrée
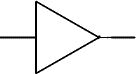
sortie
Attention
: à ne pas confondre cette porte logique avec l'ampli-opérationnel ou
encore le comparateur qui eux ont deux entrées (+ & -).
En portes européennes :entrée
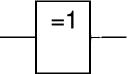
sortie
Le NON (ou inverseur)
En schématique :
Avec une table de vérité : | SW2 | | L2 |
| relaché | 0 | | allumée | 1 |
| poussé | 1 | | éteinte | 0 |
En Français :La lampe L2 est éteinte si le bouton SW2 est poussé.
(En binaire : La sortie est l'opposé de l'entrée)
En algèbre de Boole : L2 = SW2En langage de programmation Pascal :l2 := not(sw2);En portes américaines :entrée
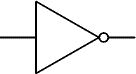
sortie
En portes européennes :entrée
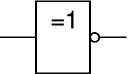
sortie
Le ET (ou AND)
En schématique :
Avec une table de vérité : | SW12 | SW11 | | L11 |
| relaché | 0 | relaché | 0 | | éteinte | 0 |
| relaché | 0 | poussé | 1 | | éteinte | 0 |
| poussé | 1 | relaché | 0 | | éteinte | 0 |
| poussé | 1 | poussé | 1 | | allumée | 1 |
En Français :La lampe L11 est allumée si le bouton SW11 et le bouton SW12 sont simultanément poussés.
En algèbre de Boole :L11 = SW11.SW12NB : attention à ne pas confondre l'opérateur boléen "." (ET) avec l'opérateur arithmétique "." (multiplication) !
En langage de programmation Pascal :l11 := sw11 and sw12;En portes américaines :entrées
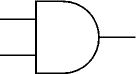
sortie
En portes européennes :entrées
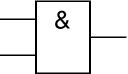
sortie
Le OU (ou OR)
En schématique :
Avec une table de vérité : | SW22 | SW21 | | L21 |
| relaché | 0 | relaché | 0 | | éteinte | 0 |
| relaché | 0 | poussé | 1 | | allumée | 1 |
| poussé | 1 | relaché | 0 | | allumée | 1 |
| poussé | 1 | poussé | 1 | | allumée | 1 |
En Français :La
lampe L21 est allumée si le bouton SW21 ou le bouton SW22 sont
poussés (l'un ou l'autre, ou encore les deux en même temps).
En algèbre de Boole :L21 = SW21 + SW22NB : attention à ne pas confondre l'opérateur boléen "+" (OU) avec l'opérateur arithmétique "+" (addition) ! Ici 1+1=1
En langage de programmation Pascal :l21 := sw21 or sw22;En portes américaines :entrées
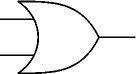
sortie
En portes européennes :entrées
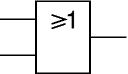
sortie
Les représentations de combinaisons logiques
Comme
nous venons de le voir dans les combinaisons de base ci-dessus, la représentation d'une combinaison de
signaux logiques peut se faire de plusieurs manières.
En schématique :
Via le dessin de l'interconnexion de contacts, de lampes, de relais, de moteurs, de transistors, de diodes LED...
Mais ne sera compréhensible que par un électronicien !
Exemple :
Avec une table de vérité :
Un tableau décrit tous les états des sorties selon toutes les combinaisons possibles des entrées.
Nombre de colonnes = nombre d'entrées + nombre de sorties.
Nombre de lignes = 2nombre d'entrées
Très complet, mais devient vite fastidieux s'il y a beaucoup d'entrées !!!
1 entrée => 2 lignes dans le tableau
2 entrées => 4 lignes dans le tableau
3 entrées => 8 lignes dans le tableau
4 entrées => 16 lignes dans le tableau
5 entrées => 32 lignes dans le tableau
6 entrées => 64 lignes dans le tableau
7 entrées => 128 lignes dans le tableau
8 entrées => 256 lignes dans le tableau
...
Pour
être certain de bien couvrir toutes les combinaisons possibles des
entrées (et pour ne pas complexifier inutilement les choses lorsque
nous passerons au système de numération binaire), procédez comme suit :
- première ligne : toutes les entrées sont inactives (0)
- changer l'entrée dans la colonne la plus à droite à chaque ligne (0 1 0 1 0 1 0 1 0 1...)
- changer l'entrée dans la colonne juste à gauche de la précédente toutes les 2 lignes (0 0 1 1 0 0 1 1 0 0 1 1 ...)
- changer l'entrée dans la colonne juste à gauche de la précédente toutes les 4 lignes (0 0 0 0 1 1 1 1 0 0 0 0 ...)
- changer
l'entrée dans la colonne juste à gauche de la précédente toutes
les 8 lignes (0 0 0 0 0 0 0 0 1 1 1 1 ...)
- changer l'entrée dans la colonne juste à gauche de la précédente toutes les 16 lignes
- ... jusqu'à atteindre la première colonne.
- si vous avez bien procédé, toutes les entrées sont actives (1) à la dernière ligne.
Pour notre exemple :
| SW33 | SW32 | SW31 | | L32 | L31 |
| 0 | 0 | 0 | | 0 | 0 |
| 0 | 0 | 1 | | 0 | 1 |
| 0 | 1 | 0 | | 1 | 0 |
| 0 | 1 | 1 | | 1 | 0 |
| 1 | 0 | 0 | | 0 | 0 |
| 1 | 0 | 1 | | 0 | 0 |
| 1 | 1 | 0 | | 0 | 0 |
| 1 | 1 | 1 | | 0 | 0 |
En Français :
C'est par exemple le cahier des charges d'un circuit à réaliser. Ou encore la description du fonctionnement d'un système.
Pour notre exemple :
L31
et L32 sont éteintes si SW33 est poussé ; sinon L32 est allumée si SW32
est inversé et L31 est allumée si SW32 est non inversé et que SW31 est
poussé.
En algèbre de Boole :
Chaque sortie est représentée par une équation logique.
Pour notre exemple :
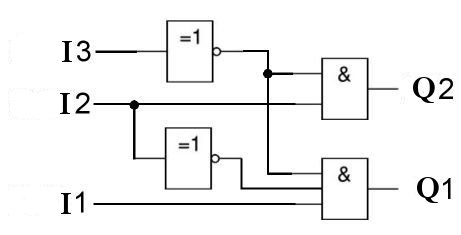
L31 = SW33 . SW32 . SW31
L32 = SW33 . SW32
En langage de programmation Pascal :
Les entrées et les sorties sont représentées par des variables (type boolean) afin de les nommer.
Chaque
sortie reçoit via le symbole d'affectation ":=" une combinaison logique
des variables d'entrées réalisée au moyen d'opérateurs binaires "not,
and, or, xor" avec possibilité de regroupements au moyen de "(
)".
Pour notre exemple :
l31 := not(sw33) and not(sw32) and sw31;
l32 := not(sw33) and sw32;
En portes américaines ou européennes :
Les entrées sont reliées aux sorties via l'interconnexion de portes logiques.
Pour notre exemple en portes américaines :
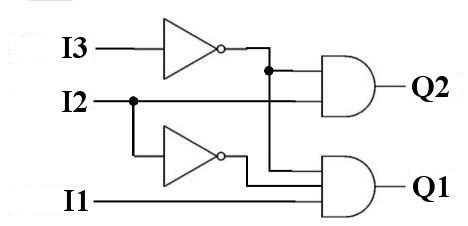
Pour notre exemple en portes européennes :
Sources des symboles de cette page : http://www.kpsec.freeuk.com/symbol.htm#logicgates
Auteur : Philippot Marc - 17/10/2010
