ISSLg
- Cours d'électronique
Comment passer d'un
schéma à une équation et inversement
Navigation> electronique/automatisme/portes/equations
Pour plus de détails,
voir Floyd - Systèmes numériques - 9ème édition :
p182 : Chap 4 : Algèbre booléenne et simplification logique
Parenthèses et priorité des
opérations
Les opérandes des AND et OR peuvent être permutées (comme en
arithmétique avec le . et le + ...)
A . B = B . A
a and b = b and a
A + B = B + A
a or b = b or a
S'il n'y a pas de parenthèses, l'ordre de priorité
d'exécution des opérateurs d'une équation est :
NOT , AND , OR , XOR (comme en arithmétique le
signe est prioritaire au . qui est prioritaire au + ...)
NB : le NOT est parfois noté comme ceci : /A = A
Pour
modifier cet ordre d'exécution il faut mettre entre parenthèses les
expressions à effectuer en premier lieu, ce seront également les
premières portes du circuit logique en symbolique US ou EU.
Il y a distributivité ou mise en évidence entre le AND et le OR (comme en
arithmétique avec le . et le + ...) :
A . (B + C) = A . B + A . C
Exemples :
S = A . B + C . D = (A . B) + (C . D)
mais est
différent de A . (B
+ C) . D
S
= /A . B + C = A
. B + C = ((A)
. B) + C mais est différent de
/(A . B) + C = (A
. B) + C
Le passage d'un schéma à une
équation
- Au besoin, redessiner le schéma pour mettre les entrées à
gauche et les sorties à droite.
- Nommer les entrées.
- Partir
des portes les plus à gauche, et écrire à leur sortie la combinaison de
leurs entrées en utilisant si nécessaire des parenthèses.
- La combinaison des entrées de la dernière porte à droite
vous donnera l'équation finale.
NB : si vous avez plusieurs sorties, il vous faudra une équation par
sortie.
Exemple :
Nommer les entrées.
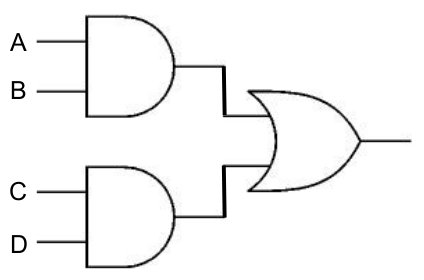
Traitement des deux porte AND à gauche.
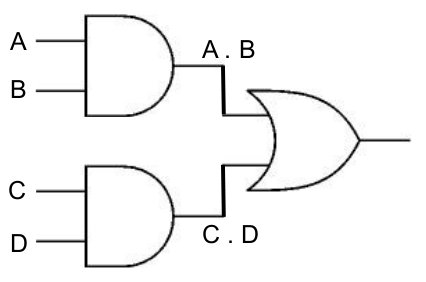
Traitement de la porte OR à droite.
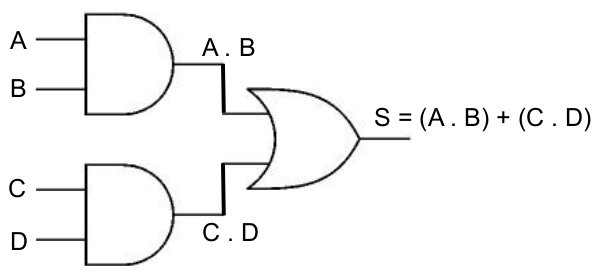
Le passage d'une équation à un
schéma
Procéder de manière inverse :
- Remettre toutes les parenthèses sous-entendues.
- Partir de la parenthèse de plus haut niveau, en tirer la
porte la plus à droite ainsi que l'équation de ses entrées.
- Remonter de la sorte vers la gauche, jusqu'au traitement de
tous les niveaux de parenthèses.
NB
: si vous avez plusieurs équations (c-à-d plusieurs sorties), vous avez
intérêt à repérer les portions d'équations commune pour simplifier le
schéma.
Exemple :
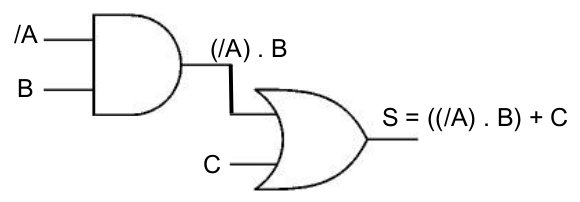
S
= /A . B + C
S = ((A)
. B) + C
Traitement du +
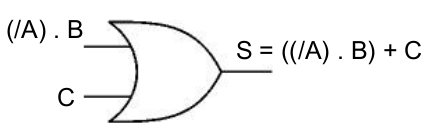
Traitement du .
Traitement du /
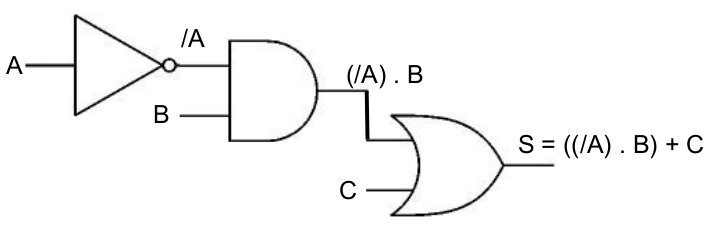
NB : Le passage d'une équation à
une table de vérité
Se fait simplement par calcul.
Exemple pour S
= /A . B + C
| C |
B |
A |
S
= /A . B + C |
| 0 |
0 |
0 |
/0 . 0 + 0 = 0 |
| 0 |
0 |
1 |
/1 . 0 + 0 = 0 |
| 0 |
1 |
0 |
/0 . 1 + 0 = 1 |
| 0 | 1 | 1 | /1 . 1 + 0 = 0 |
| 1 | 0 | 0 | /0 . 0 + 1 = 1 |
| 1 | 0 | 1 | /1 . 0 + 1 = 1 |
| 1 |
1 |
0 |
/0 . 1 + 1 = 1 |
| 1 |
1 |
1 |
/1 . 1 + 1 = 1 |
Auteur :
Philippot Marc - 24/10/2013





